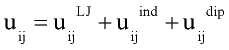
When developing an equation of state for molecular fluids one can follow two different strategies. First, it is possible to take an empirical equation of appropriate functional form and to find the values for its coefficients so as to reproduce available experimental data. The main disadvantage of this approach is that it is usually valid only in the restricted P-T range where experimental data are available.
The second possibility is to describe interaction of molecules in the fluid by an abstract physical model. Then it is necessary to construct an equation, describing the behavior of the hypothetical fluid with a chosen model of intermolecular interaction. In contrast to the empirical approach the experimental data are not used to fit coefficients of the equation but to choose a realistic model of intermolecular interaction. The basic idea is that interaction between molecules change only slightly with P and T. This means, that the model obtained using the experimental data in one P-T range will be also accurate at other P-T conditions. Last makes theoretical equations safe for extrapolations.
To develop an equation of state for a given model of intermolecular interaction, one can use molecular dynamic or/and Monte-Carlo simulations or thermodynamic perturbation theory. Moreover, there are strong connection between both ideas. Both methods benefits and suffer some limitations. In this work perturbation theory have been implemented. The physical pattern of the intermolecular interaction considered here is the model the dipolar "Lennard-Jones"-spheres.
In the next part the basic ideas of the perturbation theory are reported. We do not go far into detail, especially the ones relating to computational problems, since that can be found in the references given in the text.
The main contribution to the potential interaction energy between two polar molecules is given by the sum of Lennard-Jones, dipole-induced dipole, and dipole-dipole interaction:
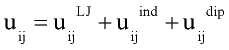
where
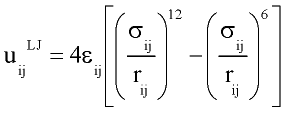
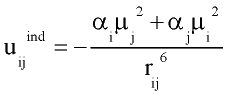
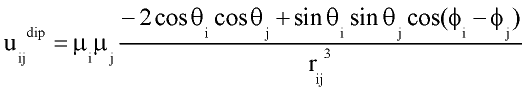
with rij distance between centers of molecules i and j; q and f are angles defining relative orientation of two dipoles fig 1; sij and eij are substance specific parameters of Lennard-Jones interaction (fig2); a is average polarizability of molecule and m its dipole moment. It is clear that, interaction between nonpolar molecules is particular case of this potential. If one of molecules has no dipole moment, uijdip=0. If both molecules nonpolar, the only nonzero term is uijLJ.
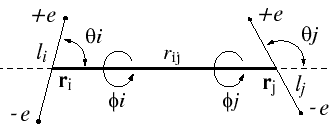
Figure 1.
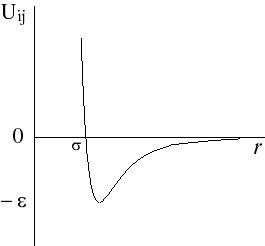
Figure 2. Lennard-Jones interaction potential.
Gray and Gubbins, 1984 used the thermodynamic perturbation theory to develop equation of state for the fluid mixtures interacting with such potential. While thermodynamic properties of the system with Lennard-Jones interaction are well known, it convenient to take Lennard-Jones system as a reference one and consider contribution from other type of interaction(dipole-dipole, dipole-induced dipole) as perturbation (deviation from properties of Lennard-Jones system). Then Helmholtz free energy A is expressed in form of power expansion:
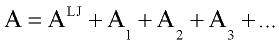
where ALJ is Helmholtz free energy of Lennard-Jones fluid and A1, A2, A3 are first, second and third order perturbation contribution.
Explicit expressions for and A1, A2, A3 in the fluid mixtures are follow (Gubbins and Twu 1978a):
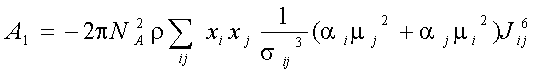
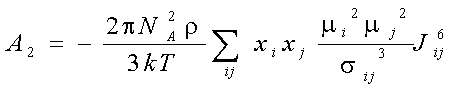
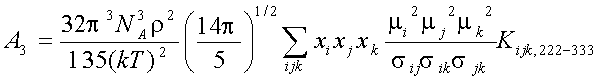
where xi -mole fraction of compound i, r -densiry , N- numder of particles, T-temperature. The symbols Jij6, and Kijk,222-333 denote integrals over pair and triple distribution function of reference Lennard-Jones fluid. Its depend on temperature, density and Lennard-Jones parameters sij and eij. The simple analytic approximation for the integrals Kijk was calculated by Gubbins and Twu (1978). Following approach of Stell G. at. al (1972), have been used to calculate Jij6 from the properties of reference system:
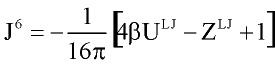
where U and Z are internal energy and compressibility of Lennard-Jones fluid.
In order to improve convergence of perturbation expansion Stell at al. (1972, 1974) recommended to use [0,1] Pade approximation for dipole-dipole interaction, which gives final expression for Helmholtz free energy of system as:
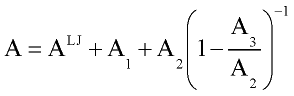
Thermodynamic properties of reference Lennard-Jones system were calculated with modified Weeks- Chandler-Andersen perturbation theory (Weeks at al., 1971; Andersen at al., 1972).:
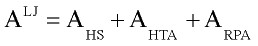
there AHS is free energy of hard sphere system ( Carnahan and Starling, 1969; Boublic 1970), AHTA is so called high temperature approximation. In current work Shmulovich, at al.(1982) results were used for AHTA. Simple analytical expression for ARPA term (random phase approximation) proposed by Miyano and Masuoka (1984). For the details of practical implementation see discussion of Verlet and Weis (1972, 1973).
Perturbation expansion discussed above give Helmholtz free energy of the system A=A(T, r) as function of temperature and fluid density. Other thermodynamic quantities of interest are derived by differentiation:
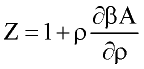
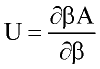
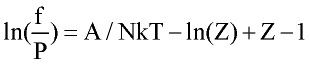

where n number of moles; f-fugacity of pure fluid; fi fugacity coefficient of compound i in the mixture. List of other important derivatives is given by Praushnitz at al (1986).
See: pdf-documentation file to GEMS-package